This project begins with the idea to implement my own C++ numerical computing platform as an analogy to MATLAB.
This repository contains necessary packages for symbolic computation, matrix algebra, etc., and also offers data visualization – graphs.
Symbolic computation is used SymbolicC++ library, for data visualization and plotting, is used Gnuplot-iostream
Optimization application
TwoDimensional::Function myFunction((x - 2)*(x + 5) + y*y);
TwoDimensional::Point startPoint(1.5, 5);
Optimization::NelderMead myMethod(myFunction, startPoint);
myMethod.findMinimum();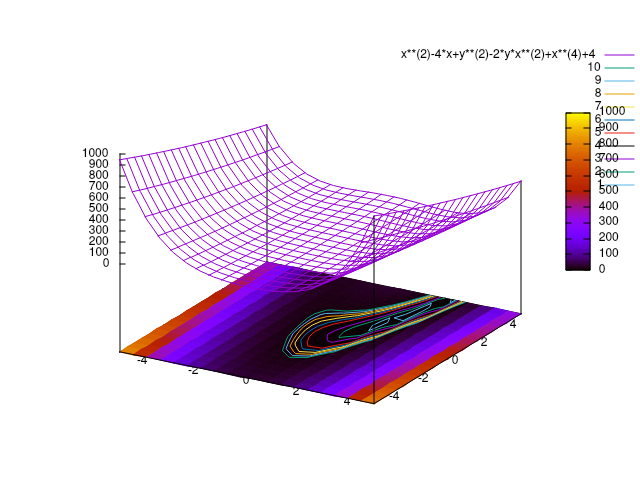
Numerical computing
Open-source Interactive numerical computing environment
Toolbox specification
This repository contains the necessary packages for symbolic computation,
matrix algebra etc., also offer data visualization – graphs.
Symbolic computation is used SymbolicC++ library, for data visualization and
plotting is used Gnuplot-iostream.
Area of use
Matrices algebra
Symbolic differential computation
Graphical solutions and visualizations
Mathematical function properties analysis
Numerical computing library
My C++ implementation of utilities is based on symbolic computation.
Point
Object Points represent points in n-dimensional space.
OneDimensional::Point myPoint(2);
TwoDimensional::Point myPoint(1.5, 5);
ThreeDimensional::Point myPoint(1.5, 2, 5);- Point value
myPoint[i];return point value ini
By callmyPoint.matrix;are possible matrices operations, return1 x n
Function
Object Function represents mathematical function by symbolic variables.
TwoDimensional::Function myFunction((x - 2)*(x + 5) + 3*y);-
Function value
myFunction.value(Point);
return function value of the function at givenPoint. -
Function gradient
myFunction.gradient(); myFunction.gradient(Point);
return matrixn x 1of function’s first derivatives – gradient. -
Function hessian
myFunction.hessian(); myFunction.hessian(Point);
return matrixn x nof function’s second’s derivatives – hessian. -
Function character of stationary/inflection point
myFunction.character(Point);
returnStationaryPoin::Minimum = 0if Point is a local minimum of a function, returnStationaryPoin::Maximum = 1if Point is a local maximum, orStationaryPoin::Saddle = 2
if Point is the saddle point of the function.
Plot
Object Plot offers graphical visualization and data plotting.
Plot::function(myFunction.getSymbolic());

My application
I have developed this platform to implement Numerical Optimization comparative and gradient methods
used for finding local extremes of functions.
Numerical optimization
One-dimensional optimization problem
- Davidon’s search
- Golden selection search
Two-dimensional optimization problem
- Nelder & Mead’s method
- Newton & Raphson’s method
- Levenberg & Marquardt method
Usage example
TwoDimensional::Function myFunction((x - 2)*(x + 5) + y*y);
TwoDimensional::Point startPoint(1.5, 5);
Optimization::NelderMead myMethod(myFunction, startPoint);
myMethod.findMinimum();